Détermination de l'enthalpie molaire standard de combustion du méthanol CH₃OH à 338 K connaissant son enthalpie molaire standard de combustion à 298 K.

Données :
 

	CH3OH (l)	O2 (g)	CO2 (g)	H2O (l)
DcH° (CH3OH, l, 298 K) (kJ mol-1)	- 726,7
CP  (J mol-1 K-1)	81,1	30	44,2	75,2
Lvap (kJ mol-1)	35,2
Tvap (K)	338

 

Remarque : 338 K est la température de vaporisation du méthanol. On peut donc envisager à cette température :

    soit la combustion du méthanol à l'état liquide

    soit la combustion du méthanol à l'état gazeux

On peut utiliser le cycle thermodynamique suivant : 

mais on peut aussi appliquer directement la loi de KIRCHOFF :

 D_cH° (CH₃OH, l, 338 K) =

D_cH° (CH₃OH, l, 298 K) + Sn _i.C_P.(338 - 298)

(les C_P étant constants) 

A.N. :

D_cH° (CH₃OH, l, 298 K) =

- 726,7 + (44,2 + 2.75,2 - 81,1 - 3/2.30).10^-3.40

=

- 726,7 + 2,74

D_cH° (CH₃OH, l, 338 K) = - 723,96 kJ mol^-1 

Dans ce cas, l'utilisation du cycle thermodynamique est indispensable pour faire apparaître le changement d'état physique du méthanol :  

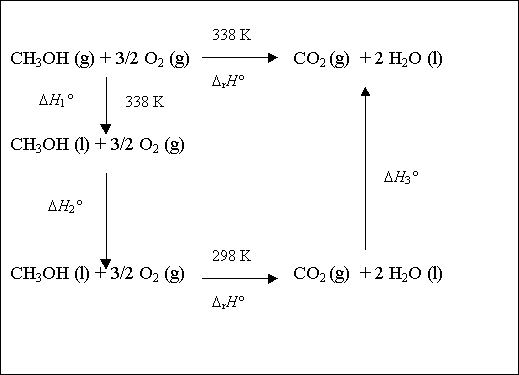
ce qui permet d'écrire :

D_rH°(CH₃OH, g, 338 K) =

DH°₁ + DH°₂  + D_rH°(CH₃OH, l, 298 K) + DH°₃

DH°₂  et DH°₃ représentent les variations d'enthalpie dues aux changements de température des réactifs et des produits

DH°₁ représente le changement d'état physique du méthanol à température constante (338 K) :

DH°₁ = - L_vap(CH₃OH, l).

A.N.

D_cH° ( CH₃OH, g, 338 K)

=

D_cH° ( CH₃OH, l, 298 K) + Sn_i.C_P.(338 - 298) - L_vap( CH₃OH)

=

- 726,7 + 2,74 - 35,2

D_cH° (CH₃OH, g, 338 K) = - 759,16 kJ mol^-1

Remarque

Par rapport à la combustion à 298 K :

 D_cH° (CH₃OH, l, 298 K) = - 726,7 kJ mol^-1

on constate que 

lorsqu'il n'existe aucun changement d'état physique D_cH° varie peu (0,4 %)

cette variation est plus importante lorsque le méthanol a changé d'état physique (4,5 %)